Böhm tree

The concept of a Böhm tree arises in lambda calculus, a discipline within mathematical logic and computer science. It is named after Corrado Böhm.

If one considers lambda-terms as trees, the set of Böhm trees is the set of all possible trees built by taking a lambda-term and replacing zero, one or more subterms by a special symbol $\bot$ , and allowing for infinite trees. It can be proved that Böhm trees are a model of lambda-calculus.

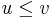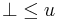Böhm trees can be ordered by the following relation : $u \leq v$ if $v$ can be obtained out of $u$ by replacing some occurrences of $\bot$ by subtrees. Clearly, every Böhm tree $u$ is such that $\bot \leq u$ . The set of Böhm trees with this ordering is a complete partial order.

Informally, starting from a lambda-term and reducing it to try to reach a normal form using the leftmost outermost evaluation strategy, we can use Böhm trees as we go as a way to represent the information obtained so far about the normal form (with the $\bot$ indicating the subterms which still need to be reduced). If the lambda-term isn't strongly normalizing, the leftmost outermost evaluation strategy will fail to terminate, and the interpretation of the lambda-term will be an infinite Böhm tree.